)
BULL
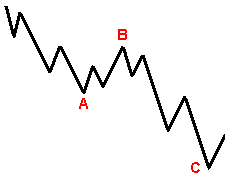 Рис.13
Рис.13
BEAR
 Рис.14
Рис.14
Волна (В) не достигает начальной точки волны (А). Волна (С) значительно перекрывает конец волны (А).
Двойной зигзаг
Часто встречается на больших моделях (М),(W).
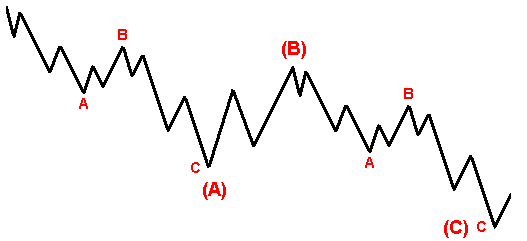 Рис.15
Рис.15
Плоские волны
Эти волны образуют конфигурацию (3 -3 -5
). Волна (А) состоит из трех волн. Плоская волна, скорее всего, консолидация, чем коррекция.
BULL
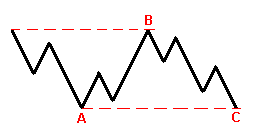 Рис.16
Рис.16
BEAR
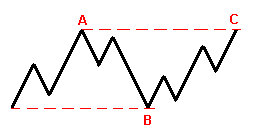 Рис.17
Рис.17
Волна (В) достигает вершины волны (А), демонстрируя более высокий рыночный потенциал. Завершающая волна (С) заканчивает свой ход у основания волны (А) или чуть ниже, и, наоборот, для медвежьего.
Два исключения плоской коррекции "неправильная" коррекция (3 - 3 - 5)
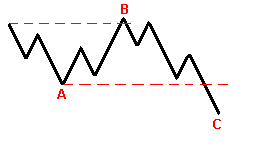
BULL
 Pис.18
Pис.18
BEAR
 Рис.19
Рис.19
Вершина волны (В) превышает верх волны (А), а волна (С) опускается ниже основания волны (А) для бычьего рынка, и, наоборот, для медвежьего.
"Перевернутая неправильная" коррекция
BULL
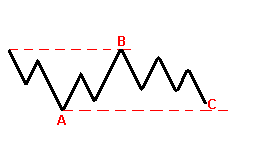 Рис.20
Рис.20
BEAR
 Рис.21
Рис.21
Волна (В) достигает вершины волны (А), в то время как волна (С) так и не опускается до уровня основания волны (А). В этом случае бычий рынок обладает более высоким потенциалом, и, наоборот, для медвежьего рынка.
Бегущая коррекция (running correction)
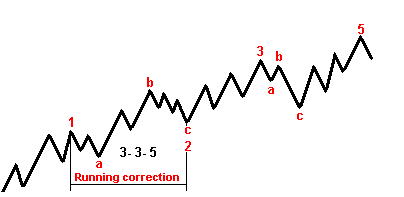 Рис.22
Рис.22
Встречается крайне редко, но появление ее на графиках свидетельствует об очень сильном потенциале рынка.
Треугольники
Обычно появляются на (4) волне. Они также могут появиться на волне (В), входящую в корректирующую конфигурацию (А) (В) (С). Таким образом, при восходящей тенденции их можно охарактеризовать как бычью, так и медвежью модель одновременно. Обычно это фигура продолжения, если это не вершина. Как правило, является продолжением существующей тенденции после еще одной волны роста.
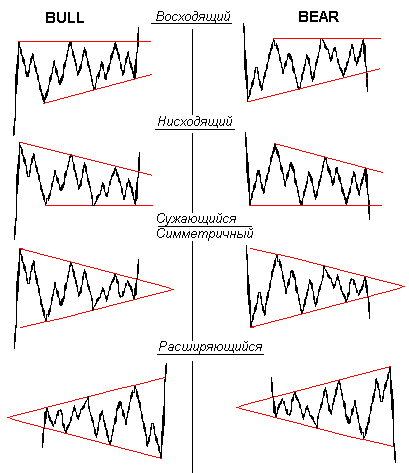 Рис.23
Рис.23
Вершина треугольника (то есть точка, в которой сходятся все линии тренда) часто соответствует моменту завершения (5) заключительной волны.
Двойные
тройки
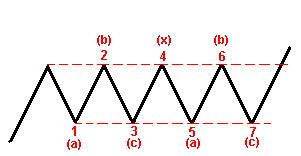 Рис.24
Рис.24
Правило чередования
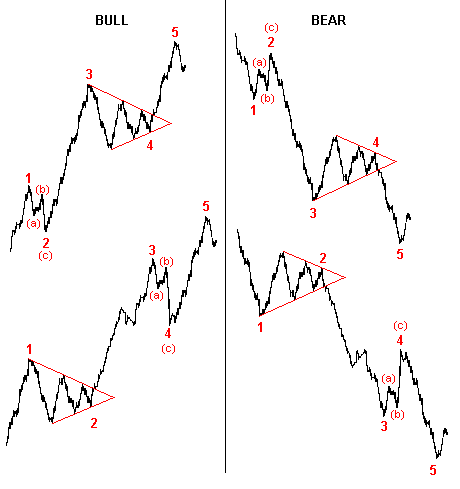 Рис.25
Рис.25
Если волна (2) представляет собой простую модель коррекции (а) (в) (с), то волна (4) скорее всего, образует треугольник, и наоборот.
Числа Фибоначчи - математическая основа теории волн
Как признавал сам Элиот в своей работе "Законы природы", математической основой теории стала последовательность чисел, которую открыл (или, чтобы быть точнее, вновь открыл) Фибоначчи в XIII веке. В его честь открытую им последовательность стали называть "числами Фибоначчи".
Фибоначчи в свое время опубликовал три большие работы, самая знаменитая из которых называется "Liber Abaci". Благодаря этой книге Европа узнала индо-арабскую систему чисел, которая позднее вытеснила традиционные для того времени римские числа. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. В "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144
(далее до бесконечности). Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых - почти постоянная взаимосвязь между числами.
Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т.д.
Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Обратите внимание, как значение соотношений колеблются вокруг величины 0,618, причем размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.
Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618и 1,618 Перейти на страницу: 6 7 8 9 10 11 12 13 14 15 16